- Planar Fourbar Linkages - Fundamental Design Parameters
- Using GitHub Issue Comments for your Website
- Valid Initial Fourbar Pose
- Publishing Math Documents Using Markdown
- Animation of the Cubic of Stationary Curvature of a Fourbar Linkage
- Maximum Area of a Fourbar Linkage
- Cross product considered harmful
- Introducing markdown-it-texmath
Planar Fourbar Linkages - Fundamental Design Parameters
A fourbar linkage is the most simple mechanism having a mobility of one and revolute joints only. It is composed of four binary links - the bars - connected to each others by four revolute joints. With respect to the latter fact it is also called 4R mechanism. Read more ...
Using GitHub Issue Comments for your Website
As of now, static web pages are quite popular. These pages here are also simple HTML documents readily published to the web server.
Static pages are not much compatible with dynamic user comments. So comment hosting services like Disqus are frequently used in combination with static web sites.
As critics regarding loading time and security with Disqus are increasing, I was attracted by a solution using GitHub hosted comments. Read more ...
Valid Initial Fourbar Pose
Analysis and simulation of fourbar mechanisms is nothing new and done for decades. The initial pose of the fourbar linkage is usually nothing, we think about very often. Solving the task to animate one cycle of a crank-rocker, we pragmatically let the crank angle start at 0° and stop at 360° (with respect to whatever). But this implies, that we know,
- that the fourbar satisfies the Grashof condition.
- which link is the fully rotatable link.
McCarthy classifies eight basic types with the fourbar. For each type we have to
- check the Grashof condition.
- identify the fully rotatable link, if any.
- choose the driven input link.
- specify an initial input angle for the input link.
- set an end angle accordingly.
Now imagine a scenario, where you can graphical interactively modify the four link lengths. Then you must go through these steps with each length change. The critical step here would be to find an always valid start angle for your input link, if one is even uniquely identified.
The universal method suggested here based on Brahmagupta's formula for finding a valid initial pose is independent of above steps.
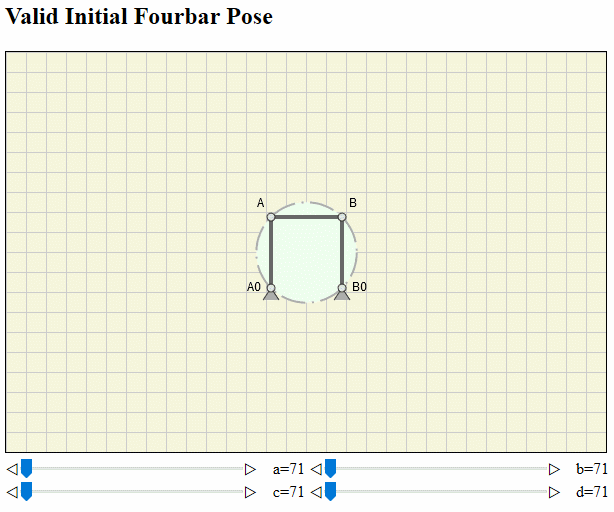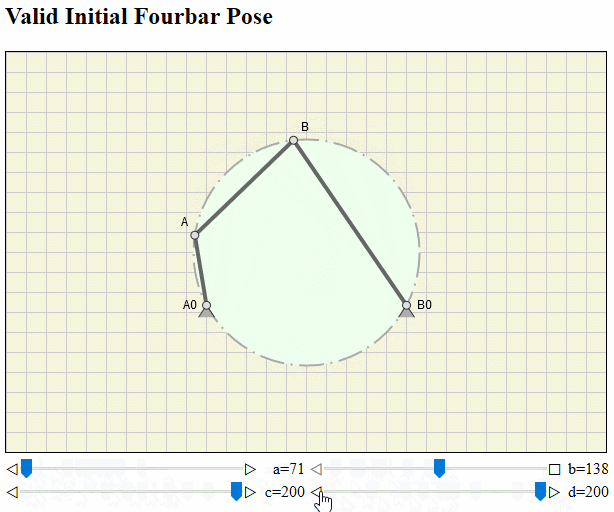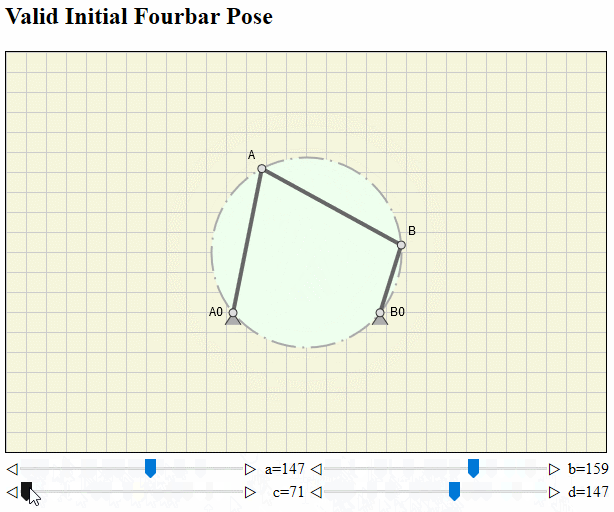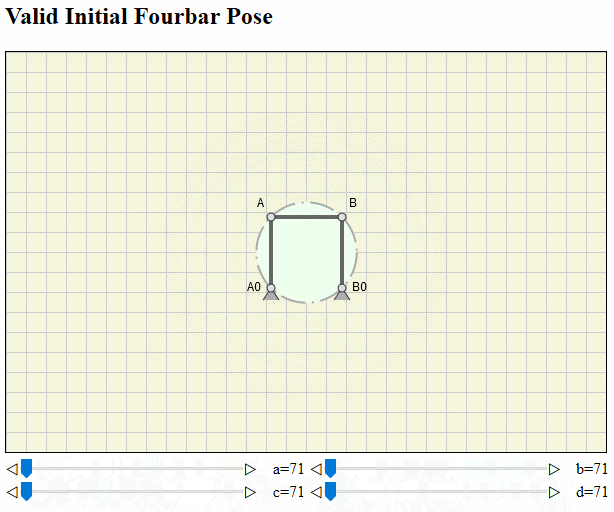
If interested you can read more about the theoretical background here on my web site, view it at Research Gate or download the pdf.
Publishing Math Documents Using Markdown
Microsoft's Visual Studio Code - not to be confused with Visual Studio - is primarily a programming editor based on cross platform Electron framework. Additionally it is also an excellent Markdown editor.
I have implemented a vscode extension mdmath a while ago for being able to use LaTeX math within markdown documents.
This extension is a comfortable tool for scientists, engineers and students with markdown as their first choice document format.
As of release 1.15 vscode provides a markdown extension API, which allows close integration with the native markdown previewer. As of release 2.0 mdmath is using this extension API as well as my markdown-it extension markdown-it-texmath.
If you want to read more about mdmath go to the or to my github repo. Download counter already reached
.
Animation of the Cubic of Stationary Curvature of a Fourbar Linkage
In mechanism analysis and design knowledge about direction and curvature of point paths on a moving link of kinematic chains proves itself valuable and was intensively studied in the past. The famous Euler-Savary equation is a central point in the discussion of these properties. We can then derive time-independent pure geometric relations from it:
- Inflection Pole
and Circle (red) - The Curve of Points of Constant Curvature (not shown here)
- The Cubic of Stationary Curvature (blue)
- Ball's Point (third point on inflection circle)
You can read more about the theoretical background here on my web site, view it at Research Gate or download the pdf.
You might also want to read some comments on Hacker News.
In a near future article I will discuss the generation of mechanical engineering related web animations.
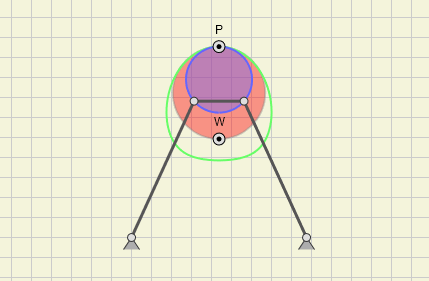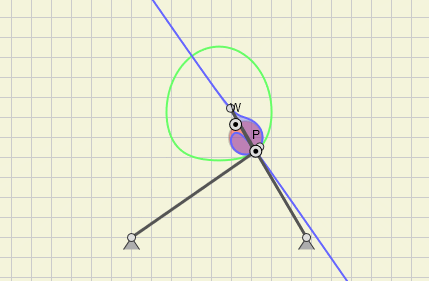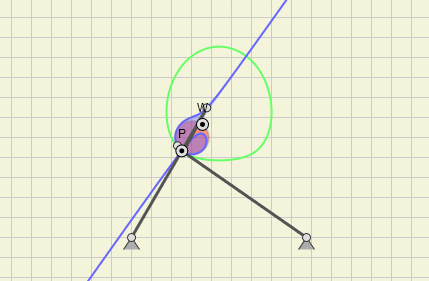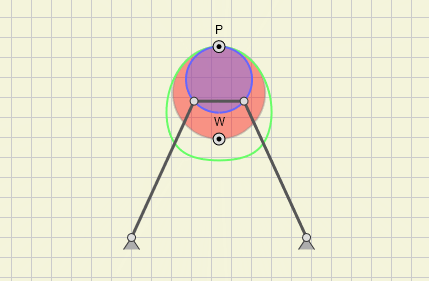
Maximum Area of a Fourbar Linkage
Planar fourbar linkages - consisting of 4 binary links and 4 revolute joints - can occur as different types:
- crank-rocker
- rocker-crank
- double-crank
- double-rocker
When such a fourbar linkage has to be drawn in an initial pose, which
- is independent of a driving link
- works for any of the four types
- looks pleasant
the question comes up, how to define such a pose.
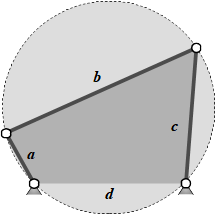
As a solution we can take a particular position, where the area of the quadrilateral built by the four joints gets maximal (Fig.).
According to the Formula of Brahmagupta - an ancient Indian mathematician - all vertices are lying on a circle then. A direct relationship to Ptolemy's theorem - another ancient Greek mathematician - exists.
In order to find the corresponding linkage position, I did a more in-depth discussion of the geometric situation, Ptolemy's theorem and Brahmagupta's formula.
Cross product considered harmful
Every now and then you may have noticed someone complaining about the fact, that algebra in vector space
B. Bantchev writes in his article Calculating with Vectors in Plane Geometry:
"The way geometry is taught in schools today has not changed significantly for quite a long time ... The vector apparatus, introduced in different forms in the 19th century by Hamilton, Grassmann, Gibbs, and others, is apparently still a new tool in geometry, and this is reflected by both teaching it and applying it."
A similar phrasing can be found at J. Angeles in his article "A novel approach to the teaching of planar mechanism dynamics":
"The teaching of the planar kinematics and dynamics of machines has undergone very few, if any, innovations in the last half century. We ... came across an alternative, novel formulation, based on an operator used to represent the three dimensional cross-product in two-dimensional form.
I am using a similar approach on a regular basis in higher education for mechanism analysis and design. You can read more about it in my article (pdf).
Note: That article was written in Visual Studio Code as a comfortable markdown editor. For math support my vscode extension Markdown+Math was used for testing and improvement.
Introducing markdown-it-texmath
markdown-it-texmath is a markdown-it extension, which allows to write math equations with TeX/LaTeX notation inside of markdown documents. You can see the visual representation of Euler's identity (1) below.
The math notation used for this equation was $$e^{i\pi} + 1 = 0$$ (1) inside of the markdown document, from which this static web page was generated.
KaTeX is used as a fast math renderer for this. You can even try it out interactively, if you want.
markdown-it was chosen because of its active developers and agile community. Having a closer look at markdown-it you might see
already a lot of math plugins.
So why implement yet another markdown-it math plugin?
- My personal preference for a Markdown Editor is Visual Studio Code - not to be confused with Visual Studio.
- As there is no native support in
vscodefor rendering math formulas, I implemented Markdown+Math as avscodeextension - based on KaTeX - a while ago. - As Markdown+Math is a vscode extension, but not a true plugin for
markdown-itat current, I decided to turn it into one. Advantages to have amarkdown-itplugin are:- Possibility of using it independent of
vscodein the browser and withnode.js. - Ensuring better future integratability with
vscode.
- Possibility of using it independent of
markdown-it-texmathcan also render formula numbers, which was a critical requirement for me.
So, if you want to know a little more about markdown-it-texmath and/or mdmath, go to my GitHub repos.