Valid Initial Pose of Any Fourbar Linkage

Stefan Gössner

August 23, 2017

Department of Mechanical Engineering, University of Applied Sciences, Dortmund, Germany.

Keywords: Fourbar Linkage; Brahmagupta's formula; cyclic quadrilateral; initial pose;

Abstract

For simulating fourbar linkages a valid initial pose is needed. Finding such a pose is sometimes a non-trivial task. In this paper an elementary method for specifying a valid initial pose of any fourbar linkage is suggested.

Introduction

Analysis and simulation of fourbar mechanisms is nothing new and done for decades. The initial pose of the fourbar linkage is usually nothing, we think about very often. Solving the task to animate one cycle of a crank-rocker, we pragmatically let the crank angle start at 0° and stop at 360° (with respect to whatever). But this implies, that we know,

• that the fourbar satisfies the Grashof condition.
• which link is the fully rotatable link.

McCarthy classifies eight basic types with the fourbar [1]. For each type we have to

• check the Grashof condition.
• identify the fully rotatable link, if any.
• choose the driven input link.
• specify an initial input angle for the input link.
• set an end angle accordingly.

Now imagine a scenario, where you can graphical interactively modify the four link lengths. Then you must go through these steps with each length change. The critical step here would be to find an always valid start angle for your input link, if one is even uniquely identified.

The universal method suggested here for finding a valid initial pose is independent of above steps.

Prerequisites

The geometric shape of a fourbar mechanisms is a quadrilateral in every pose. The area enclosed by that quadrilateral becomes extreme, when it is a cyclic quadrilateral. Brahmagupta's formula helps to calculate the aera $A$ enclosed by that cyclic quadrilateral as well as the radius $R$ of the circle, all vertices are lying on [2].

Let's take as an assumption, that the fourbar's pose corresponding to a cyclic quadrilateral is always a valid pose.

The maximal area of a cyclic quadrilateral is determined by

with the semiperimeter

The radius $R$ of the corresponding circle is then [2]

Please note, that Brahmagupta's Formula is of no help to draw the cyclic quadrilatral's shape, i.e. providing the side vectors or the angles between the sides.

The qadrilateral shape corresponding to the fourbar pose is to be determined with given side lengths $a, b, c, d$ only.

The vectorial method applied is making use of an orthogonal operator. The orthogonal vector to $\\bold a$ is denoted here as $\\tilde\\bold a$, while in other publications it is often written as $\\bold a^{\\perp}$ [3].

Calculate the Fourbar Pose

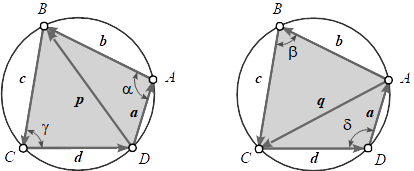
We start analog to the proof of Brahmagupta's Formula with the sum of the area of the two triangles in Fig.1 using half area product each [2] .

Both angles in the triangles opposite to each diagonal sum up to $180^{\\circ}$, i.e.

The perp dot products of the side vectors correspond to the sines of the enclosed angles, so we can write

Introducing these expressions to equations (4) we get for the sine's

The dot products of the side vectors correspond to the cosines of the enclosed angles, so we can write

Now expressing the diagonal vectors by its two triangle side vectors each

and squaring leads us to

Reintroducing these expression to equations (6) yields the cosines

With this we have all ingredients to determine the side vectors $\\bold a,\\bold b,\\bold c, \\bold d$. Let the base vector $\\bold d$ be aligned with the positive x-axis. The side vectors then finally result using expressions (5) and (7).

Please note, that trigonometric functions were used here only for clarification. The resulting vector equations (8) describing the initial pose are trigonometry-free.

References

[1] J.M. McCarthy, G.S. Soh, Geometric Design of Linkages, Springer, 2010.
[2] Brahmagupta's Formula, S. Gössner.
[3] Cross Product Considered Harmful, S.Gössner.